• A tree is a non-linear structure
• A tree is great to represent hierarchical information
• Tree is a direted graph
• At the top of the tree, a special node called root. Root is the only node that does not have incoming edges
• All other nodes have exactly 1 incoming edge
• Each node can have an arbitrary number of outgoing edges

• If n is a node and it is connected to n₁, n₂, ..., n_k via outgoing edges, then n₁, n₂, ..., n_k are all children of n, and n is called the parent
• Nodes which do not have any outgoing edges are called leaves
• A node which is neither a root nor a leaf is called internal
• Internal nodes are those nodes that have a parent and at least 1 child
• Nodes in a tree can be arranged by levels, root is at level 0, level 1 contains all children of root, ...
• There is exactly 1 path from the root to any given node
• The children of a given node are ordered from left to right: first child, second child, third child, ...
• Given a node n, the set of nodes which have n as ancestor represents a tree structure called subtree rooted at n
• The degree of a tree is the maximum number of children that each node is allowed to have

• Binary tree is a tree with a degree of 2
• Each node can have at most 2 children
• First child of a node is called the left child
• Second child of a node is called the right child
• A binary tree where each node has 2 children except for the leaves is called complete binary tree

• All the nodes to the left of a node n have a less value then the value at node n
• All the nodes to the right of a node n have a greater value than the value at node n

#!/usr/bin/python
""" A model containing Node class """

__author__ = "Lin Chen"
__version__ = "0.1"

class Node:
    """Single node in the binary search tree"""

    def __init__(self, data):
        """Initialize a Node
        
        Args:
            data : data saved in the node
        """
        self._data = data
        self._left = None
        self._right = None
        self._parent = None

    @property
    def data(self):
        return self._data

    @data.setter
    def data(self, d):
        self._data = d

    @data.deleter
    def data(self):
        del self._data

    @property
    def left(self):
        return self._left

    @left.setter
    def left(self, n):
        self._left = n

    @left.deleter
    def left(self):
        del self._left

    @property
    def right(self):
        return self._right

    @right.setter
    def right(self, n):
        self._right = n

    @right.deleter
    def right(self):
        del self._right

    @property
    def parent(self):
        return self._parent

    @parent.setter
    def parent(self, n):
        self._parent = n

    @parent.deleter
    def parent(self):
        del self._parent

    def __str__(self):
        return str(self._data)
			

#!/usr/bin/python
""" A model containing Binary Search Tree"""

from NodeModule import Node

class BST(object):
    """Class of binary search tree"""

    def __init__(self):
        """Initialize a binary search tree
        """
        self._root = None

    @property
    def root(self):
        return self._root

    @root.setter
    def root(self, n):
        self._root = n

    @root.deleter
    def root(self):
        del self._root

    def isEmpty(self):
        return (self._root is None)

    def size(self):
        return self.getSize(self._root)

    def getSize(self, n):
        if n is None:
            return 0

        return 1 + self.getSize(n.left) + self.getSize(n.right)

    def height(self):
        return self.getHeight(self._root)

    def getHeight(self, n):
        if n is None:
            return 0
        if n.left is None and n.right is None:
            return 1

        l = self.getHeight(n.left)
        r = self.getHeight(n.right)

        h = 1+l if l > r else 1+r

        return h

    def inorderWalk(self):
        """Print elements in ascending order, O(n)"""
        if self._root is not None:
            self.printLDR(self._root)
            print()

    def printLDR(self, n):
        if n is None:
            return
        self.printLDR(n.left)
        print('<'+str(n)+'>', end = ' '),
        self.printLDR(n.right)

    def preWalk(self):
        """Print element in pre-order, O(n)"""
        if self._root is not None:
            self.printDLR(self._root)
            print()

    def printDLR(self, n):
        if n is None:
            return
        print('<'+str(n)+'>', end = ' '),
        self.printDLR(n.left)
        self.printDLR(n.right)

    def postWalk(self):
        """Print element in pre-order, O(n)"""
        if self._root is not None:
            self.printLRD(self._root)
        print()

    def printLRD(self, n):
        if n is None:
            return
        self.printLRD(n.left)
        self.printLRD(n.right)
        print('<'+str(n)+'>', end = ' '),

    def search(self, v):
        """Search if a value has been saved in the binary search tree
        
        Returns:
            Node, return the node containing the value if find it in tree, None otherwise"""
        if self._root is not None:
            return self.searchTree(self._root, v)

    def searchTree(self, n, v):
        if n is None or v == n.data:
            return n
        if v < n.data:
            return self.searchTree(n.left, v)
        else:
            return self.searchTree(n.right, v)

    def min(self):
        """Return node containing minimum value in the binary search tree"""
        n = self.getMin(self._root)
        return n

    def getMin(self, n):
        if n is None or n.left is None:
            return n
        return self.getMin(n.left)

    def max(self):
        """Return node containing maximum value in the binary search tree"""
        n = self.getMax(self._root)
        return n

    def getMax(self, n):
        if n is None or n.right is None:
            return n
        return self.getMax(n.right)

    def successor(self, v):
        """Return the node with the smallest key greater than v"""
        n = self.search(v)
        if n is None:
            return None

        return self.getSuccessor(n)

    def getSuccessor(self, n):
        if n.right is not None:
            return self.getMin(n.right)
        y = n.parent
        while (y is not None) and (n is y.right):
            n = y
            y = y.parent
        return y

    def predecessor(self, v):
        """Return the node with the largest key less than v"""
        n = self.search(v)
        if n is None:
            return None

        return self.getPredecessor(n)

    def getPredecessor(self, n):
        if n.left is not None:
            return self.getMax(n.left)
        y = n.parent
        while (y is not None) and (n is y.left):
            n = y
            y = y.parent
        return y

    def insert(self, v):
        if self.search(v) is not None:
            return

        p = None
        current = self._root

        while current is not None:
            p = current
            current = p.left if v < p.data else p.right

        n = Node(v)
        n.parent = p

        if p is None:
            self._root = n
        else:
            if v < p.data:
                p.left = n
            else:
                p.right = n

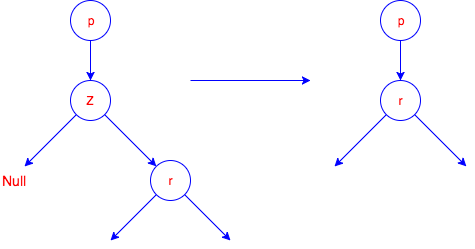
    def transplant(self, u, v):
        """Replaces the subtree rooted at node u with the subtree rooted at node v"""
        if u.parent is None:
            self._root = v
        elif u == u.parent.left:
            u.parent.left = v
        else:
            u.parent.right = v
        if v is not None:
            v.parent = u.parent

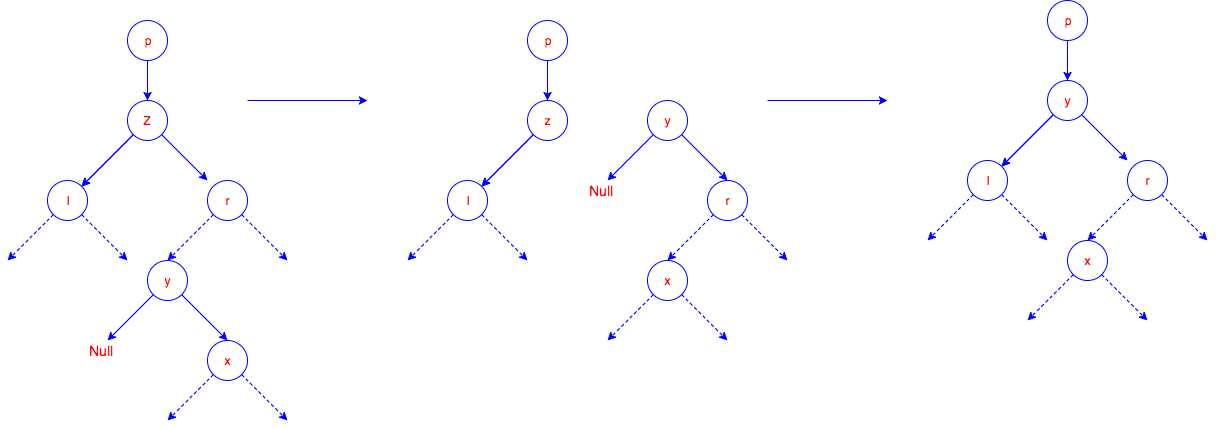
    def delete(self, e):
        """Delete the node which contains data e"""
        z = self.search(e)

        if z is None:
            return;

        if z.left is None:
            self.transplant(z, z.right)
        elif z.right is None:
            self.transplant(z, z.left)
        else:
            y = self.getMin(z.right)
            if y.parent != z:
                self.transplant(y, y.right)
                y.right = z.right
                y.right.parent = y
            self.transplant(z, y)
            y.left = z.left
            y.left.parent = y
			

Node has right child

Node has no right child

Node has left child

Node has no left child

Node has no children, remove it by modifying its parent to replac the node with None as its child

Node has just one child, take the node's position in the tree by modifying the node's parent to replace the node by the node's child

Node has two children, find the node's successor. Have the successor take the node's position in the tree. The rest of the ndoe's original right subtree becomes the successor's new right subtree, and the node's left subtree becomes the successor's new left substree

Node has only right child, or has no child

Node has only left child

Node has two children

#!/usr/bin/python

from BSTModule import BST

def main():
    t = BST();

    # Create tree
    t.insert(8);
    t.insert(3);
    t.insert(10);
    t.insert(1);
    t.insert(6);
    t.insert(14);
    t.insert(4);
    t.insert(7);
    t.insert(13);
    t.insert(15);

    # Display tree
    t.inorderWalk()
    t.preWalk()
    t.postWalk()

    # size
    print('Size: ', t.size())

    # height
    print('Height: ', t.height())

    # search
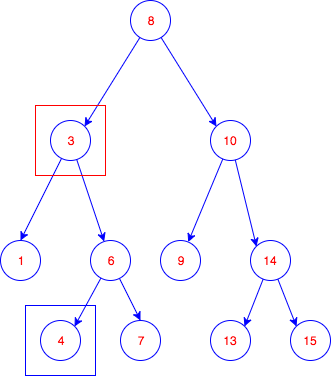
    print(t.search(7)) # 7
    print(t.search(20)) # None

    # min
    print(t.min()) # 1

    # max
    print(t.max()) # 15

    # successor
    print(t.successor(3)) # 4
    print(t.successor(7)) # 8
    print(t.successor(8)) # 10
    print(t.successor(15)) # None

    # predecessor
    print(t.predecessor(13)) # 10
    print(t.predecessor(10)) # 8
    print(t.predecessor(8)) # 7
    print(t.predecessor(1)) # None

    # delete
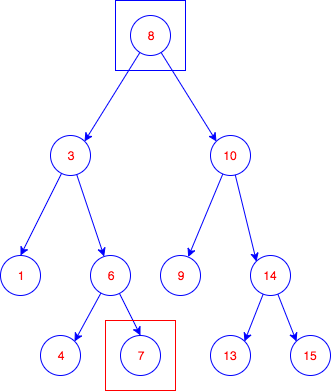
    t.delete(3);
    t.inorderWalk();

if __name__ == '__main__':
    main()
			

• CLRS
• Geeksforgeeks