Single-Source Shortest Paths
- Given a weighted, directed graph G = (V, E), search the shortest-path from start vertex s to each vertex v ∈ V
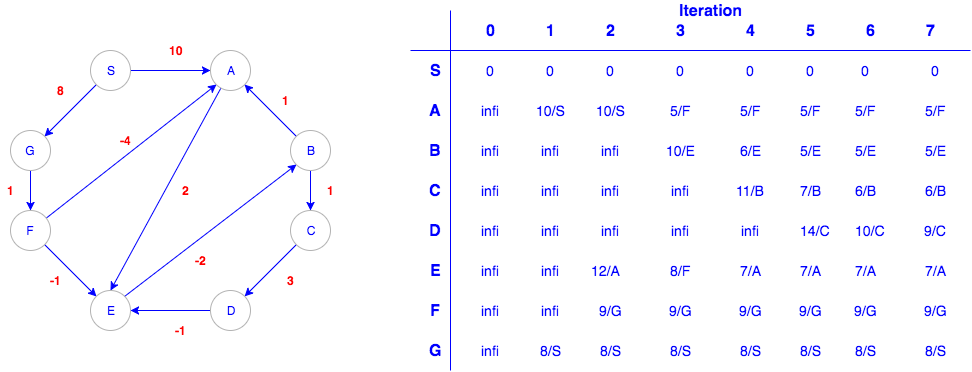
Bellman-Ford Algorithm
- Allow negative edge weight
- Dynamic Programming
- O(VE)
- Each node v has v.d for a shortest-path estimate, v.π for its parent
- For each edge (u, v), if (u.d + w(u, v)) < (v.d), update v.d and v.π
- Repeat above step |V|-1 times
- If there is any edge has (u.d + w(u, v)) < v.d, the graph exit negative-weight cycle, there is no shortest path
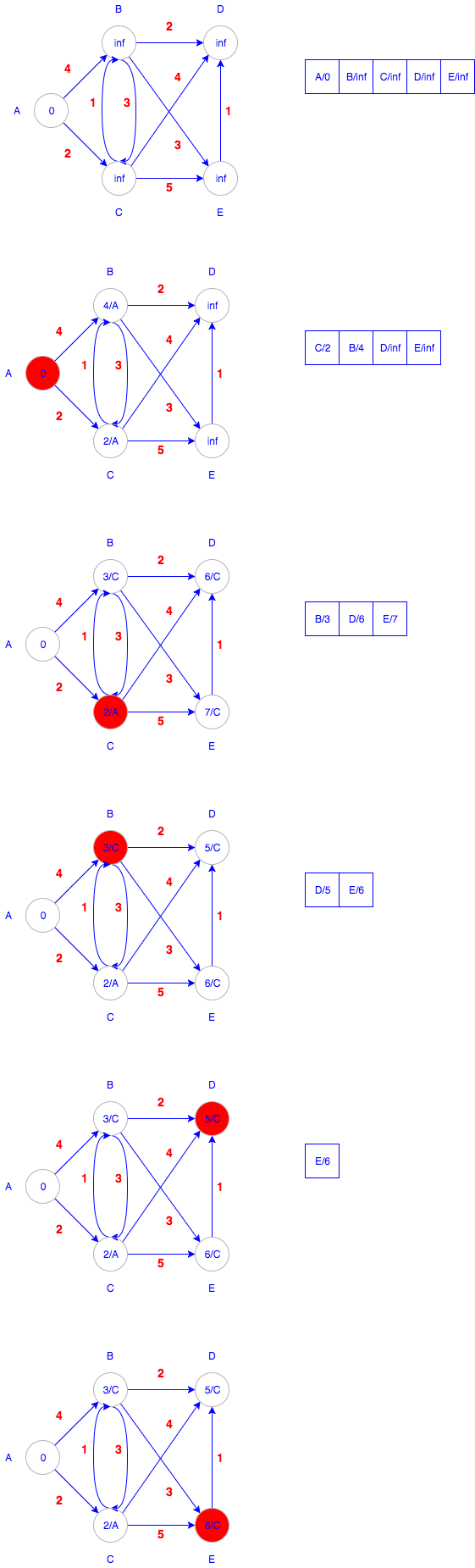
Single-Source Shortest Paths in Dag (Directed Acyclic Graph)
- Use DFS to check the finish time for each node
- List all nodes by finish time to form a dag
- For each node u in the list, check each edge (u, v), if (u.d + w(u, v)) < v.d, update v.d and v.π
- Repeat for each node in the list in order
Dijkstra's Algorithm
- Greedy algorithm
- Edge weights are nonnegative
- O(VlgV + E)
- Each node v has v.d for a shortest-path estimate, v.π for its parent
- Set the edge weight of all nodes to be infinite, push them into a min-priority queue
- Set the edge weight of the start node to be zero
- Pop node u from queue, check all edge (u, v), if (u.d + w(u, v)) < v.d, update v.d and v.π
- Repeat until the queue is empty
Reference