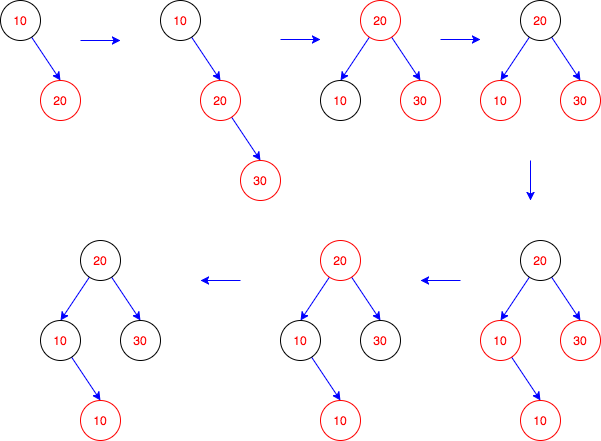
Red-Black Tree
- Every node has a color either red or black
- Root of tree is always black
- Every leaf is black
- There are no two adjacent red nodes (A red node cannot have a red parent or red child)
- Every path from root to a NULL node has same number of black nodes
Rotation
Insertion
- O(lgn)
- Perform standard BST insertion and make the color of newly inserted nodes as RED
- If x is root, change color of x as BLACK
- Do following if color of x’s parent is not BLACK or x is not root
- if uncle is RED
- Change color of parent and uncle as BLACK
- color of grand parent as RED
- Change x = x’s grandparent, repeat until parent is black or x is root
- if uncle is BLACK
Deletion
- O(lgn)
- y's color is BLACK, x's color is BLACK
- x's sibling w is red
- set w to be BLACK
- x's parent to be RED
- left rotate x's parent
- this converts case 1 to case 2/3/4
- x's sibling w is BLACK, and both of w's children are BLACK
- set w to be RED
- x's parent to be new x
- x's sibling w is BLACK, w's left child is red, and w's right child is black
- set w's left child to be BLACK, w to be RED
- right rotate w
- set new x's sibling as w
- x's sibling w is BLACK, w's right child is red
- set w to be x's parent's color
- set x's parent's color to be BLACK
- set right child to be BLACK
- left rotate x's parent
- y's color is BLACK, x's color is RED
- Set x's color to be BLACK
Reference