Dynamic Program
Steps
- Characterize the structure of an optimal solution
- Recursively define the value of an optimal solution
- Compute the value of an optimal solution, typically in a bottom-up fashion
- Construct an optimal solution from computed information
Properties
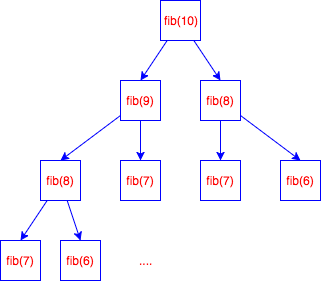
- Overlapping Subproblems
- Optimal Substructure
Navie Fibnacii
public class Fibonacci
{
public static int fib(int n)
{
if(n <= 1)
return n;
else
return fib(n-1) + fib(n-2);
}
public static void main(String args[])
{
System.out.println(fib(100));
}
}
Memoization Fibnacii, Top Down
public class Fibonacci
{
int memory [];
public Fibonacci(int n)
{
memory = new int[n+1];
for(int i = 0; i < n+1; i++)
memory[i] = -1;
}
public int fib(int n)
{
if(memory[n] == -1)
{
if(n <= 1)
memory[n] = n;
else
memory[n] = fib(n-1) + fib(n-2);
}
return memory[n];
}
public static void main(String args[])
{
Fibonacci f = new Fibonacci(40);
System.out.println(f.fib(40));
}
}
Tabulation Fibnacii, Bottom Up
public class Fibonacci
{
public static int fib(int n)
{
int [] array = new int[n+1];
array[0] = 0;
array[1] = 1;
for(int i = 2; i <= n; i++)
array[i] = array[i-1] + array[i-2];
return array[n];
}
public static void main(String args[])
{
System.out.println(fib(30));
}
}
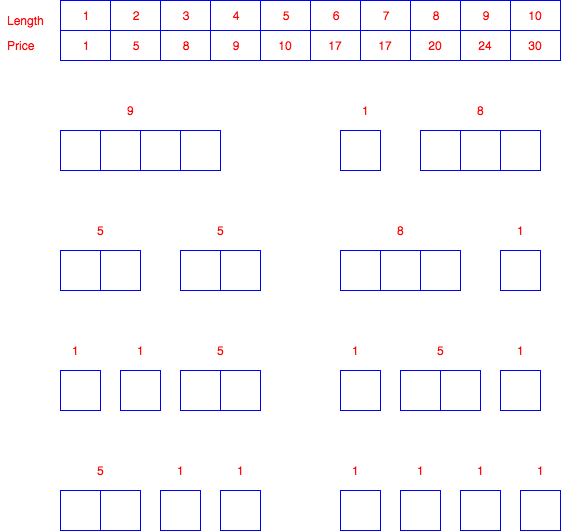
Rod-cutting problem
- Cut rod into k pieces, n = i1 + i2 + ... + ik
- Maximum revenue, rn = p[i1] + p[i2] + ... p[in]
- Cut a rod into i (left-hand end) and n-i (right-hand end), only the right-hand end is divided
- rn = max(pi + rn-i)
- Reference
public class C
{
public static int cutRod(int prices [], int n)
{
if (n <= 0)
return 0;
int max_val = Integer.MIN_VALUE;
for (int i = 0; i<n; i++)
max_val = Math.max(max_val, prices[i] + cutRod(prices, n-i-1));
return max_val;
}
public static void main(String args[])
{
int prices [] = {1, 5, 8, 9, 10, 17, 17, 20, 24, 30};
System.out.println(cutRod(prices, 5));
}
}
//Memorization
public class C
{
public static int cutRod(int prices [], int n, int r [])
{
if(r[n] > 0)
return r[n];
if (n <= 0)
return 0;
int max_val = Integer.MIN_VALUE;
for (int i = 0; i<n; i++)
max_val = Math.max(max_val, prices[i] + cutRod(prices, n-i-1, r));
r[n] = max_val;
return max_val;
}
public static void main(String args[])
{
int prices [] = {1, 5, 8, 9, 10, 17, 17, 20, 24, 30};
int r [] = new int[prices.length+1];
System.out.println(cutRod(prices, 10, r));
}
}
//Tabulation
public class C
{
public static int cutRod(int prices [], int n)
{
int [] val = new int[n+1];
val[0] = 0;
for(int j = 1; j <= n; j++)
{
int max_val = Integer.MIN_VALUE;
for (int i = 0; i<j; i++)
{
max_val = Math.max(max_val, prices[i] + val[j-i-1]);
}
val[j] = max_val;
}
return val[n];
}
public static void main(String args[])
{
int prices [] = {1, 5, 8, 9, 10, 17, 17, 20, 24, 30};
System.out.println(cutRod(prices, 4));
}
}
Reconstructing a solution
- sj, the optimal size of the first piece to cut off
public class C
{
public static void cutRod(int prices [], int n, int val [], int s [])
{
for(int j = 1; j <= n; j++)
{
int max_val = Integer.MIN_VALUE;
for (int i = 0; i<j; i++)
{
if(max_val < prices[i] + val[j-i-1])
{
max_val = prices[i] + val[j-i-1];
s[j] = i+1;
}
}
val[j] = max_val;
}
}
public static void main(String args[])
{
int prices [] = {1, 5, 8, 9, 10, 17, 17, 20, 24, 30};//price for 1, 2, 3, 4, ...
int [] val = new int[prices.length+1];//optimal price
int [] s = new int[prices.length+1];//optimal first cut off
cutRod(prices, prices.length, val, s);
for(int i = 0; i < prices.length; i++)
System.out.printf("Rod Size %2d: Price: %2d First Cut: %2d Optimal Value: %2d\n", i+1, prices[i], s[i+1], val[i+1]);
}
}
Reference